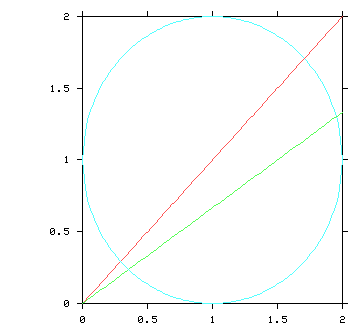
Find the value of m that minimizes the average square distance between the data y value and the y-coordinate of the curve.
Is m=1 optimal?
Solution using maple:
| postscript | maple session file | gif |
Solution using Maxima(aka Macsyma):
| text file
The optimal m is 2/3. Bear this in mind whenever someone uses least squares fitting!