|
|
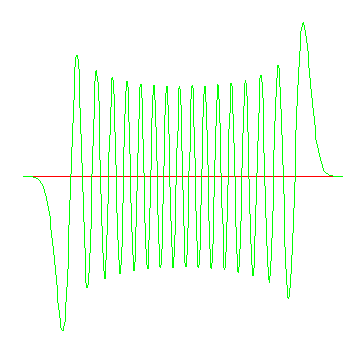
|
with(orthopoly): plot( H(31,x) * exp(-x**2/2), x = -10..10 ); |
|
|
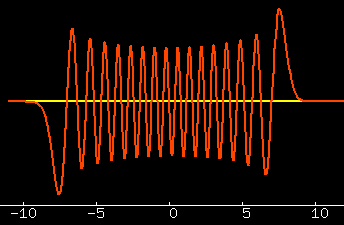
|
load("specfun")$
plot2d( hermite(31,x) * exp(-x^2/2.0),[x,-11,11]);
quit();
|

|
There are certain skills that we expect professional Physicists to use when learning and problem-solving. For example, we expect final-year Physicists, as a matter of course,
These skills are so useful to the learning of Science, it is essential that they be acquired at the beginning of the Natural Sciences tripos. I believe that working with computers now has a similar status to the skills listed above. Using a computer can be like sketching graphs - an aid to the intuition, a tool to test and refine conjectures, and a device for visualizing models. |
We have a choice of when to teach computer programming: late or early. In Part II or Part 1B - or even Part 1A.
|
I think we should teach programming early. A 2nd-year Physicist who can program effortlessly and spontaneously will be able to use computers to help learn their 2nd-year Physics. Just as we expect physicists to sketch graphs unprompted, we should aspire to teach computing so that our students naturally program while they learn. |
Let me illustrate this point with examples drawn especially from the second-year course. (Just to clarify: These are examples where fluency in computers is helpful for understanding physics; they are not proposals for activities in a computing course.)
One tricky concept in second-year physics is dispersion. Another is the idea that any displacement has a Fourier decomposition. An excellent way to understand these two issues is to simulate the ripples in a long one-dimensional shallow tank. A single pulse can be decomposed into a superposition of sinusoids, each moving at its own velocity. Add these sinusoids up again, and check, first, at time zero, do I recover the pulse? Then at subsequent times, what happens? How do the crests of the wave move relative to the packet? As the wave-packet evolves, can part of the packet be characterized as lower-frequency, and part as higher?
As an undergraduate doing wave-tank practicals, I teamed up with another student, one who was more fluent with computers, and we generated pages and pages of printouts of evolving ripples.
It was awesome to see a simple superposition of infinitely-long travelling sinusoids turning into this complex localized wavepacket. A miracle!
Such a computer program instantly lends itself to interesting variations: one can change the dispersion relation to simulate wave-packets in deeper water, for example.
To avoid any misunderstanding, let me say this: Nothing beats a real physics experiment, and I would never suggest replacing the real wave-tank experiment by experiments on the computer simulation.
But the experience of seeing a simple linear superposition of sinusoids reproduce the complexities of water-waves was a profound learning experience for me.
Understanding is a creative process: we understand by creating the subject for ourselves - by building a model of reality. Writing programs builds such a model, and one where every component is understood.
A stone's throw from `waves' is `dynamics'. Here again a simple computer plot can give huge insight into the key idea of superposition. One can plot curves to understand beats. One can decompose displacements of masses and springs into superpositions of eigenvectors. One can discover how appropriate superpositions of stationary waves create moving waves or wave-packets.
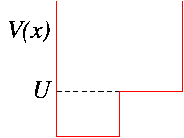
1. What does the 30th excited state of the harmonic oscillator look like?
2. What do the quantum states of a wonky well look like? Especially states with energies a little below and a little above the step-height, U?
Such questions can certainly be answered without computers, and I'd hope that all our graduating students could do so. But I believe that students grappling with quantum mechanics can gain a lot from computer-aided solution of these problems. When the computer handles the nitty-gritty of satisfying boundary conditions and so forth, the struggling intuition can focus on interesting questions like `where is the amplitude of the wavefunction bigger?' Careful reflection on computer-generated graphs can be most rewarding.
|
|
Simulate motion of planet around sun by direct solution of Newton's laws. (Use a simple method, no numerical packages.) Get an appreciation for the speed of the planet as a function of time - a detail lost from a static picture of an ellipse on the page. Get an appreciation for where the sun is, in that ellipse! Notice whether conserved quantities are conserved. Compare alternative simple methods - for example, the leapfrog method (alternate updating of position and momentum, instead of simultaneous updates) - to get a feel for the way in which small algorithmic details can make a big difference. Explore the effect of non-inverse-square forces. Understand the continuum connecting ellipses to parabolae and hyperbolae. Understand Rutherford scattering as just another example of the same thing.
SuggestionWe should have a substantial computer-programming course at the beginning of 2nd-year Physics. The course could emphasize projects that explore ideas that were covered in the 1st-year course. One aim would be for students to have `aha!' moments in which the computer exercise helps them better understand things that they didn't understand in the first year. |