Comments concerning a particular class of resonance decays:

These comments apply to the variabls mTBound, mTStar and mTTrue. This page exists to support the web-page documenting the C++ code that can be used to calculate them.

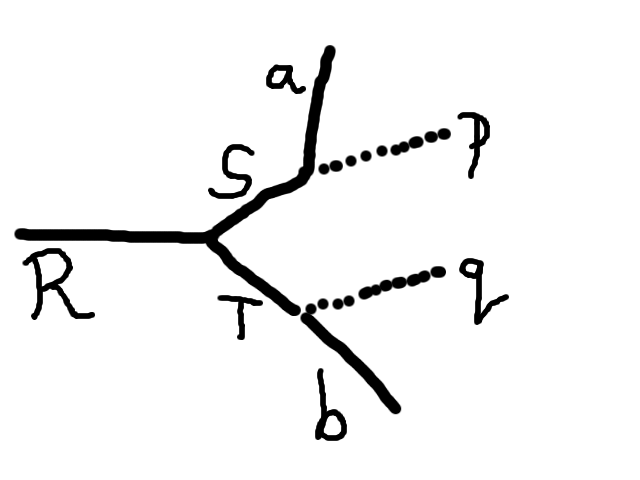
Consider the decay depicted above, in which a resonance "R" decays via two intermediate particles "S" and "T" in to four final state particles (or collections of particles) "a", "p", "q" and "b". In this decay, it is assumed that the particles (or particles) represented by "a" and the particle (or particles) represented by "b" are visible in the detector, whereas those represented by "p" and "q" are invisible, eg neutrinos. Assume that we cannot observe p and q, but we can observe "ptmiss", and let us consider only the case in which ptmiss is equal to the vector sum of the transverse components of p and q ... i.e. there are no other invisible particles in the event.

Example 1: Higgs -> tau tau -> jets nu jets nu

a=jets, b=jets, p=nus, q=nus, S=tau, T=tau.

Example 2: Higgs -> WW -> l nu l nu.

This decay mode is available if mH is greater than 2 mW.
a=lep, b=lep, p=nu, q=nu, S=W, T=W.

Example 3: Higgs -> WW* -> l nu l nu.

This decay mode is available if mH is greater than mW.
a=lep, b=lep, p=nu, q=nu, S=W, T=W*.

Example 4: Higgs -> "BLOB" -> l nu l nu.

In this last example, the identities of the "internals" have been hidden by a blob, so we do not talk of S and T specifically. Here we only see the final state particles (those that are visible) and the final state missing transverse momentum.

Mass bounds variables that may be calculated:

Assuming that both internal particles (S and T) are on-mass-shell -- eg examples 1 and 2 above

To calculate the greatest possible lower bound on the mass of the resonance R assuming that "a", "b", "p" and "q" are the only decay products of the resonance, and that both "S" and "T" are on mass shell at a specified mass, use the variable "mTBound", also known as "mTLower" or "mTLowerBound".

Assuming that both internal particles (S and T) are on-mass-shell -- eg examples 1 and 2 above

To calculate the least possible upper bound on the mass of the resonance R assuming that "a", "b", "p" and "q" are the only decay products of the resonance, and that both "S" and "T" are on mass shell at a specified mass, use the variable "mTUpper", also known as "mUpperBound".

Assuming that at least one internal particle (S or T) is on-mass-shell -- eg example 3 above

To calculate the greatest possible lower bound on the mass of the resonance R assuming that "a", "b", "p" and "q" are the only decay products of the resonance, and that at least one of "S" and "T" is on mass shell at a specified mass, use the variable "mTStar".

Assuming nothing about the internals -- eg example 4 above

To calculate the greatest possible lower bound on the mass of the resonance R, assuming nothing about the internals of the decay (i.e. not assuming anything about S and T ... i.e. ssuming that "a", "b", "p" and "q" are the only decay products of the resonance) use the variable "mTTrue".

Notes

Note 1:

It is possible for there to be no valid "mTUpper" or "mTLower" for an event. This can happen if there is a manifest incompatibility between the observed momenta, and the assumptions being made. If the event is one of these "incompatible" ones, then implementation in mTBound.h or mTLowerAndUpperBound.h should return the value -10.

Note 2:

There is one circumstance in which a negative value can be legitimately returned by one of the variables (see Note 1 above). In all other cases, the returned valies from these implementations should be non-negative. If negative values are seen, these should be treated as flags indicative of some kind of error in the library. If you see any of them, you should report them to Christopher Lester and Alan Barr with a simple standalone program that reproduces the problem.